マイナスの数はなぜ必要？

数は物を数えることから始まり（自然数）、次に数の間で足し算・引き算を導入すると、大変便利であるということに人々は気づきました。

しかし、自然数の世界だけでは計算の結果がうまく表せないことにも気づくのです。

（例１）バナナ３本とバナナ５本を合わせると

$$3+5=8$$

８個のなり、足し算は自然と計算ができます。

（例２）バナナ５本からバナナ３本を取ると

$$5-3=2$$

２個残ります。これもOK。

（例３）バナナ３本からバナナ５本を取ると

$$3-5$$

は計算ができません。

そこで誕生したのがマイナス（負）の数でした。マイナスを導入すると

$$3-5=-2$$

と計算ができます。

しかし、$-2$個のバナナなんて現実にはありませんよね。それなのにマイナスの数を考えるのはなぜでしょうか？この理由について考えていきましょう。

実生活において便利だから

バナナ－２個はイメージが付きませんが、これをお金の計算にしてみましょう。

（例）３万円の貯金があり、５万円使うと（例えばクレジットカードの後払いで）

$-2$円の赤字となります。

プラスは黒字（利益）、マイナスは赤字（負債）

として考えることができるので、便利で分かりやすいですね。

またある地点Oを基準に東（右）の方向をプラス、西（左）の方向をマイナスとします。

東に６ｋｍに移動したあと、西に１０ｋｍ移動したとき

$$6-10=-4$$

これは東に$-4$ｋｍ、つまり西に$4$ｋｍの位置にいることになります。

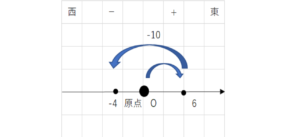
これは高校数学で登場するベクトルの考え方ですね。

気温を表す温度計、株価の値動き、海抜の表示、家計簿の赤字・黒字など

簡単にまとめましたが、いかがだったでしょうか？

マイナスの数を導入すると日常生活でも考えやすくなる問題がたくさんありますね。

歴史的に見ても、マイナスは「不条理な数」や「仮想的な数」として認められなかった数です。

（方程式の解ｘ＝-2が解として認められなかった時代もあります）

これを解決したのが、かの有名なルネ・デカルトです。数直線は彼が導入したものです。