【分数シリーズ】①分数・小数
の意味

小学校で学習するわり算。分数・小数になると難しい。
こういった声を聞くことがよくあります。
今回は分数・小数(わり算)の考え方・意味について解説していきます。
苦手な方はぜひ、見てみてください。
かけ算の逆がわり算
かけ算もわり算も、1あたりの数をもとに考えます。ざっくりいうと
- かけ算は「1あたりのものの、いくつ分」を計算すること
- わり算は「いくつ分から、分けられた1あたり」を計算すること(1の逆算)
以下、タイルを使って図解します。タイルは黄色、もしくは赤色インクが入った箱だと思ってください。
(例1)かけ算 1×6=6,2×3=6


左図の1あたりは1として、その6つ分を計算
右図は1あたりを2として、その6つ分を計算
(例2)わり算 6÷3, 1÷2

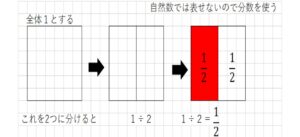
左図…分けられた1あたりが2になりますね。
右図…今度は全体が1になります。これを2つに分ける。
自然数で表せないときに分数を使います。もしくは小数0.5でも同じです。
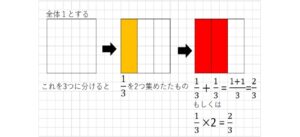
(例3)わり算 \(\frac{2}{3}\)
下図のように「1を3で割ったものを2つ集めた図」として解釈することができます。
式で書くと\(\frac{2}{3}=(1÷3)×2\)
一方で\(\frac{2}{3}\)はあくまで「2を3つにわけたもの」。上図では理解できません。
そこで、\(\frac{2}{3}=(1×2)÷3\)として解釈してみましょう。
かけ算と割り算の順序を逆にしています。
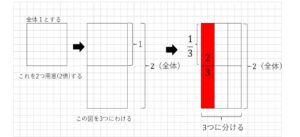
図的な意味は違いますが計算の結果は同じです。このことも押さえておきましょう。
最後に分数の分母・分子についてまとめておきましょう。
- 分母の数→「いくつに分けらているか」を見ることができる
- 分子の数→「分けられたうちの何個分か」を見ることができる
小数
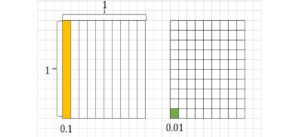
小数は分母が10、100、1000…という数をもつ特別な分数と考えてください。
(例1)\(0.1=1の\frac{1}{10}\),\(0.01=1の\frac{1}{100}\)
(例2) \(0.47=0.4+0.07\) (\(0.4=1の\frac{4}{10}\),\(0.07=1の\frac{7}{100}\))
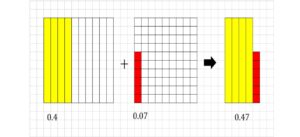
- 0.1は1を10個にわけたものの1つ分
- 0.01は1を100個に分けたものの1つ分
まとめ
かけ算やわり算(分数・小数)について解説してみました。
わり算はものを分けるときに役立つ計算ということがおわかりいただけたと思います。
図のイメージを持っておくと、理解がしやすいと思いますので、ぜひ参考にしてみてください。
次回は分数計算について解説していきます。


コメント