【整数】約数の見分け方

今回は「約数」（やくすう）いついてです。意味をおさらいすると、

約数：ある整数を割り切ることができる整数

です。

（例）４の約数

1から4まで順に割り算をしていきます。

4÷１＝４あまり０…〇　割り切れる

4÷２＝２あまり０…〇　割り切れる

4÷３＝１あまり１…×　割り切れない

4÷４＝４あまり０…〇　割り切れる

（答）１，２，４

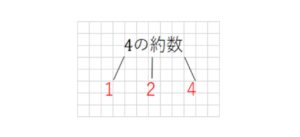
通常、このように１から順に確認していきますが、数字が大きくなると、すべて確認するのは難しいです。

（問）１２の約数

同様に計算してみてください。

（答）１，２，３，４，６，１２

図のように、「中央を基準にペアを取ってかけると12になる」という性質があります。

これを知っておくと、1から12まで順にすべて計算しなくてもよいので便利です。

（補題）３の約数

３÷１＝３あまり０…〇　割り切れる

３÷２＝１あまり１…×　割り切れない

３÷３＝１あまり０…〇　割り切れる

（答）１，３

このように「１と自分自身（＝3）」を約数にもつものを、素数（そすう）といいます。

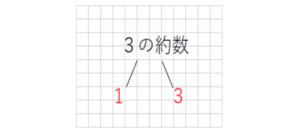
このように足が2本だけ出ているイメージですね。素数は約数は2個だけ持ちます。

少し話がそれましたが、本題に移りましょう。

下1桁での数で判定するもの　○○○○☆

2の倍数

２の倍数（偶数）の判定方法：下1桁（一の位）が２で割り切れる

⇒下一桁の数が2,4,6,8,0である

（例１）３１６

３１６の下1桁（一の位）の６は２で割り切れる。（6÷2＝3あまり０）

したがって、３１６も２で割り切れる。（316÷2＝158あまり０）

（例２）５１９０

５１９０の下1桁（一の位）が0である。

したがって、５１９０も５で割り切れる。（5190÷5＝1038あまり０）

5の倍数

５の倍数の判定方法：下1桁（一の位）が５で割り切れる

⇒下一桁の数が5,0である

（例１）１２４２１５

１２４２１５の下1桁（一の位）の5は5で割り切れる。（5÷5＝1あまり0）

したがって、１２４２１５も５で割り切れる。（124215÷5＝24843あまり0）

（例２）１２４２１０

１２４２１０の下1桁（一の位）が０である。

したがって、１２４２１０も５で割り切れる。

10の倍数

10の倍数の判定方法：下1桁（一の位）が0

（２の倍数・５の倍数の判定方法から導かれますね！）

（例）８１９２７０

８１９２７０の下1桁が０である。

したがって、８１９２７０も10で割り切れる。（819270÷10＝81927あまり0）

下２桁での数で判定するもの　○○○☆☆

４の倍数

４の倍数の判定方法：下２桁が４で割り切れる

（例１）１２４２８４

１２４２８４の下２桁８４は４で割り切れる。（84÷4＝21あまり0）

したがって、１２４２８４も４で割り切れる。（124284÷４＝31071あまり0）

下３桁での数で判定するもの　○○☆☆☆

８の倍数

８の倍数の判定方法：下３桁が８で割り切れる

（例１）７２４２８８

７２４２８８の下３桁２８８は８で割り切れる。（288÷8＝36あまり0）

したがって、７２４２８８も８で割り切れる。（724288÷8＝90536あまり0）

各位での数で判定するもの　☆☆☆☆☆

３の倍数

３の倍数の判定方法：各位の和が３で割り切れる

（例）１２３

１２３の各位の和（1+2+3）6は3で割り切れる。（6÷3＝2あまり0）

したがって、１２３も3で割り切れる。（123÷3＝41あまり0）

９の倍数

９の倍数の判定方法：各位の和が９で割り切れる

（例）１２３２１

１２３２１の各位の和（1+2+3+2+1）9は3で割り切れる。（9÷3＝3あまり0）

したがって、１２３２１も9で割り切れる。（12321÷9＝1369あまり0）

組み合わせて判定するもの

６の倍数

６の倍数の判定方法：①下１桁が２の倍数　②各位の和が３で割り切れる

２の倍数でありながら、３の倍数である数は６の倍数であるといえます。

ですので、２の倍数でありながら、３の倍数である数を確認すればよいです。

（例）３１２１２

①３１２１２の下1桁（一の位）の２は２で割り切れる。（2÷2＝1あまり０）

したがって、３１２１２も２で割り切れる。（31212÷2＝15606あまり０）

②３１２１２の各位の和（3+1+2+1+2）9は3で割り切れる。（9÷3＝3あまり０）

したがって、３１２１２も３で割り切れる。（31212÷3＝10404あまり０）

①と②より、３１２１２は６の倍数であるといえる。

まとめ

以上、2,3,4,5,6,8,9の倍数の判定方法でした。

7の倍数以外は簡単にチェックができるようになります。

高校の教科書に載っている内容なのですが、倍数の判定方法は覚えておくと、すごく便利です。

小学生のうちからぜひ覚えておきたいものですね。