【分数シリーズ】②分数の計算(通分なし・約分)

分数シリーズの続きです。
前回の内容を学習された後、読まれると良いかと思います。
今回は分数の計算(主に通分なし・約分)についてです。
分数の四則計算・約分(通分なし)
分母が同じ数の時の四則計算について見ていきます。
(例)\(\frac{1}{3}+\frac{1}{3}+\frac{1}{3}\)
まず全体が1の正方形を用意し、これを3つに分けます。
\(1÷3=\frac{1}{3}\)ですね。
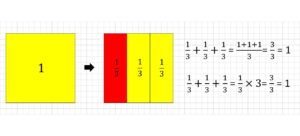
赤色の部分は、「1を3つに分けたうちの、1つ分」という意味ですから、
\(\frac{1}{3}\)を表します。これが3つ分あるので、
$$\frac{1}{3}+\frac{1}{3}+\frac{1}{3}=\frac{1+1+1}{3}=\frac{3}{3}=1$$
もしくは
$$\frac{1}{3}+\frac{1}{3}+\frac{1}{3}=\frac{1}{3}×3=\frac{3}{3}=1$$
となります。
最後に\(\frac{3}{3}\)の分母・分子を3で割っています。
これを約分といいます。
以上が、分数の足し算・かけ算の仕組みです。
引き算は、足し算の逆をたどっていけばOKです。
分母・分子に同じ数をかけても、大きさは同じ
(例)\(\frac{2}{3}=\frac{4}{6}=\frac{6}{9}=\)…
\(\frac{2}{3}\)の分母・分子に2をかけると、
$$\frac{2}{3}=\frac{2×2}{3×2}=\frac{4}{6}$$
とできますし、3をかけた場合は
$$\frac{2}{3}=\frac{2×3}{3×3}=\frac{6}{9}$$
とできます。
約分の逆の計算ですが、これはどういう意味なのでしょうか?
(図解)(1)\(\frac{2}{3}\)
「1を3つに分けたうちの、2つ分」という意味ですから、

このように表すことができます。
(2)\(\frac{4}{6}\)
(1)の図を横に真っ二つに分けてみましょう。
3つのエリアに分けられていたのが、2倍の6つに分けられています。(3×2=6個のエリア)
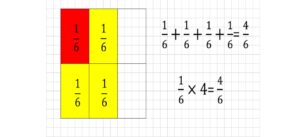
赤色の部分は「1を6つに分けたうちの、1つ分」ですから、\(\frac{1}{6}\)を表します。
黄色のエリア(=\(\frac{2}{3}\))は、\(\frac{1}{6}\)の4つ分なので、
$$\frac{2}{3}=\frac{1}{6}+\frac{1}{6}+\frac{1}{6}+\frac{1}{6}=\frac{4}{6}$$もしくは
$$\frac{2}{3}=\frac{1}{6}×4=\frac{4}{6}$$
になっています。
つまり計算するときは、分母分子に2をかけて、
$$\frac{2}{3}=\frac{2×2}{2×3}=\frac{4}{6}$$
とできるわけですね。
(3)\(\frac{6}{9}\)
(1)の図を横に三等分してみましょう。
3つのエリアに分けられていたのが、3倍の9つに分けられています。(3×3=9個のエリア)
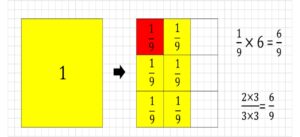
赤色の部分は「1を9つに分けたうちの、1つ分」ですから、\(\frac{1}{9}\)を表します。
右の正方形の黄色のエリア(=\(\frac{2}{3}\))は、\(\frac{1}{9}\)の6つ分なので、
$$\frac{2}{3}=\frac{1}{9}+\frac{1}{9}+\frac{1}{9}+\frac{1}{9}+\frac{1}{9}+\frac{1}{9}=\frac{6}{9}$$もしくは
$$\frac{2}{3}=\frac{1}{9}×6=\frac{6}{9}$$
になっています。
ですので、分母分子に3をかけて、
$$\frac{2}{3}=\frac{2×3}{2×3}=\frac{4}{9}$$
とできます。
まとめ
「分数の分母分子に同じ数をかける」意味が理解できましたでしょうか?
「分けられたエリアをさらに等分する計算」であることが、図からわかると思います。
エリアを分けているだけなので、求めている部分は同じですね。
単純な計算だけでなく、こういう図のイメージを持っておくと良いです(^^)
次回は、通分ありの分数計算について、解説していきます。


コメント