分数シリーズ】③分数の計算（通分あり）

続分数シリーズ。

これまでの内容を学習された後、読まれると理解が深まるかと思います。

今回も分数の計算（通分あり）についてです。

分数の足し算（通分あり）

分母の数が同じだと、分子の数どうしを足したり引いたりできます。

（例１）$\frac{3}{6}+\frac{2}{6}$

1が6つに分けられています。

分けられている数が同じなので、分子の数どうし足し算できます。

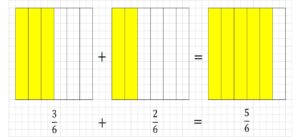
引き算もOKです。

（例２）$\frac{2}{3}+\frac{1}{4}$

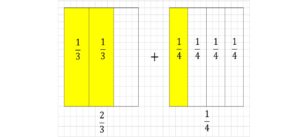
左は３分割、右は４分割されているので、そのままでは計算ができません。

これをそろえましょう。

分母が同じだと分子どうし計算ができるので、分母の数を揃えることが重要ですね。

前回出てきた通分を使います。

通分とは分母・分子に同じ数をかけてもOKというものでしたね。

それぞれ、３と４をかけると、

$$\frac{2×4}{3×4}+\frac{1×3}{4×3}$$

$$=\frac{8}{12}+\frac{3}{12}$$

$$=\frac{8+3}{12}=\frac{11}{12}$$

図的には、左の正方形は横に4分割、右の正方形は横に3分割されます。

（いずれも12のエリアに区切られます）

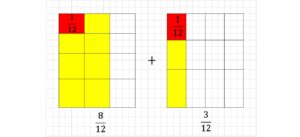
1つ分が$\frac{1}{12}$でそろったので、分子の数どうしで計算可能ですね。

今回はここまでとします。